当我们在一张平面地图上查看一条看似弯曲的航线时,一个常见的疑问是:这条线在地球上真的是“直线”吗?答案是肯定的。这条看似弯曲的路径,在地球球面上其实是两点之间最短的路径,即测地线。它在平面地图上呈现为曲线,根本原因在于:将球面展开为平面时,必然会产生扭曲。
1. 地图投影的“原罪”:扭曲
我们日常使用的世界地图(例如常见的墨卡托投影)是一个将球面“压扁”在平面上的结果。这个过程就像剥开一个橙子,并试图将果皮平铺在桌上——它必然会被拉伸或撕裂。
在墨卡托投影中,这种扭曲表现为:
- 纬度越高,拉伸越严重:为了保持“正形”,即保持方向和角度不变,地图必须随着纬度升高,将同样大小的实际区域在水平方向上拉伸得越来越大。这就是为什么格陵兰岛在地图上看起来和非洲差不多大,而实际上非洲面积是格陵兰的14倍。
2. 克莱罗定理:地球“直线”的导航法则
那么,一条在球面上的“直线”是如何受这种扭曲影响的呢?这需要用到一个18世纪的优美定理——克莱罗定理(Clairaut's Theorem)。这个定理描述了在旋转体表面(如地球)上,测地线所必须遵循的规律。
克莱罗定理的核心内容是:
在任何一个光滑的旋转体表面上,一条路径是测地线(局部最短路径)的充要条件是:路径上任意一点“到旋转轴的距离” 乘以“路径方向与经线夹角的正弦值(sin(方位角))” 保持恒定。
用公式表达即:
R × cos(纬度) × sin(方位角) = 常数
其中:
R 是地球半径。cos(纬度) 代表了该点到地球旋转轴的距离。方位角 是指路径方向与正北方向(经线方向)的夹角。
3. 定理如何解释地图上的曲线?
克莱罗定理揭示了一个关键机制:为了保持上述乘积为常数,纬度和方位角必须此消彼长,动态调整。
我们举一个例子来理解这个过程:
- 假设一架飞机从北京(约北纬40度)出发,沿着一条测地线飞行,初始方位角是东偏北30度。
- 根据克莱罗定理,此时有一个固定的“角动量”值被确定:
cos(40°) × sin(30°) ≈ 0.383。
- 如果飞机继续飞行,纬度升高(例如接近北纬73度),那么
cos(纬度) 的值会变小(因为越靠近极点,离地轴越近)。
- 为了保持乘积恒定,
sin(方位角) 的值必须增大。计算表明,当纬度到达约73度时,方位角必须增加到90度,即飞机必须变为完全向正东飞行。
结论就是:为了在球面上保持“直线”飞行,飞机的航向必须持续地向右调整(从30度不断增加到90度甚至更大)。
4. 回到地图:为什么我们看到的是一条曲线?
现在,我们把这一动态过程投射到墨卡托地图上:
- 在墨卡托投影中,经线被绘制为彼此平行的竖直线。
- 飞机的真实航向在不断地向右调整(方位角持续增大)。
- 在地图上看,这意味着飞机的路径相对于这些固定的、垂直的经线,在持续地向右弯曲。
因此,这条在三维球面上完美的“直线”,在二维地图上就呈现为一条凸向赤道的优美曲线。这不是因为飞机在转弯,而是因为地图的绘制规则,强行将球面上的几何关系“翻译”到了平面上,而克莱罗定理则精准地描述了这种“翻译”所带来的视觉变形。
如下图所示,模拟了一颗围绕地球旋转的卫星,将轨迹绘制在二维地图上的效果。
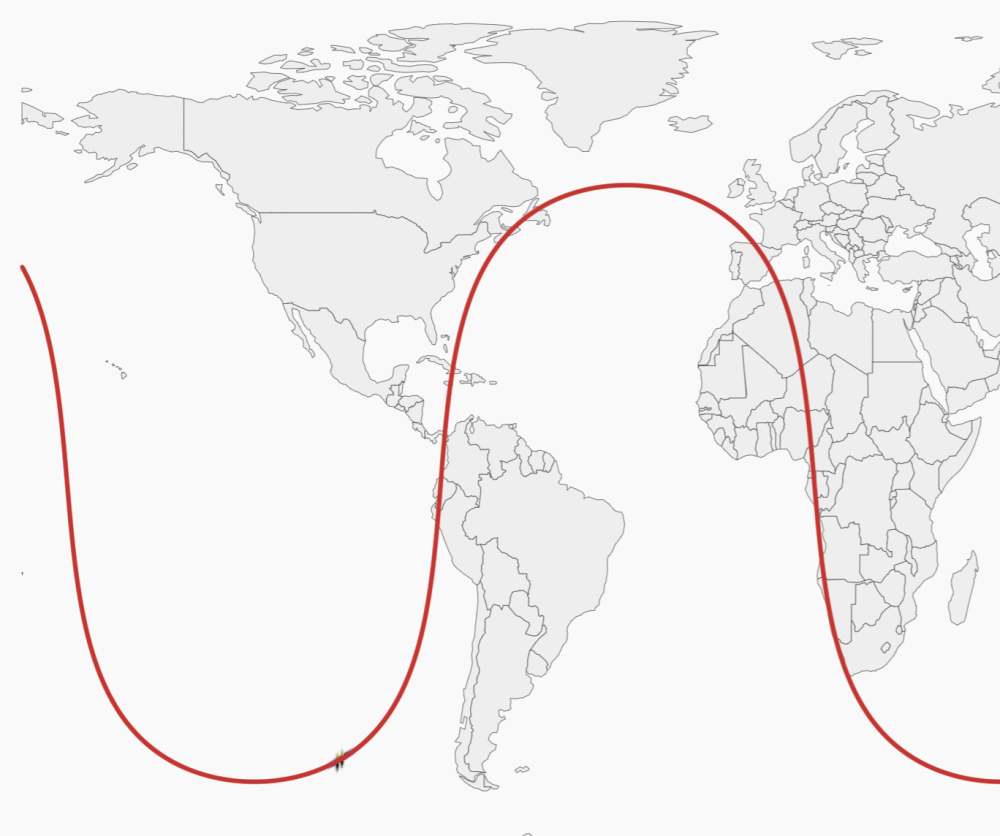
知识拓展
赤道和经线:它们是这个规则的特例。赤道上任意点的方位角为90度,经线上的方位角为0度或180度,都能满足克莱罗定理的恒定值,因此它们在地球上是测地线,在墨卡托地图上也能被画成直线。
更多GIS基础原理讨论,欢迎留言或联系我们。转载须注明出处。